みのむしクリップ
最新記事 by みのむしクリップ (全て見る)
- 2024年コンサート事情 /猫の日の思い出 - 2025年3月26日
- キャリーオーバー発生中は、外れた証 - 2025年3月25日
- ニート、車をリースする - 2025年3月24日
- 戦闘能力、タウリン4万 - 2025年3月23日
- 技術部の壺の中 – Vol. 133 [アンバサダーの恐怖] - 2025年2月28日
最近、社内の掲示板に数学系のクイズが出題された。引っかけとかではなく、真面目な数学問題。
正四面体の図形の問題は、斜辺と対角の関係が関数みたいで面白いかなと思った。
最近、テレビで見る問題は連想ゲームみたいな問題で、問題というよりはパズルゲームに近いと思う。
算数でも数学でも単純なトリックみたいなことは、よくある。
時にそれは、ケアレスミスとしてミスとされる。
寓話で
~全村人が災害対応で避難して、自分達の人数を数えたら、一人少ない。
おかしい。一人迷子になったのだろうか。
誰が数えても、登録されている人数から一人少ない。
きっと、誰かが犠牲になったんだ・・・。
避難場所に到着して、避難場所の係の人が数えたら、人数ぴったりいる。
おお、誰だかわからないけれど、無事到着していたんだ。
名乗らないけど、ひたむきなその人を祝おう。~
って、数えている自分を入れていなかったというようなマジックが、数学にはあったりする。
科学のモルとか、そういう感じ。
100mlの溶液を水を入れて1リットルに薄める。この時10倍に薄まっているけど、水は900mlで、10倍の水が必要ではない。
当たり前のことなんだけど、自分の体積分は加算されて100ml / (100ml + 900ml) = 10%見たいな感じ。
全体がα+(1-α) と言う関係式は、結構ある。
[問題]
A地点からB地点を行きは時速4Km、帰りは時速6Kmで歩くと平均時速はいくつになるか。ただし、B地点に着いたらすぐ折り返し、A地点からB地点は同じ経路を移動したものとする。
なんとなく、4 + 6 = 5Kmかなって思いたくなる。
でも、時間軸があるので、そうもいかない。
時間を無視した問題は、
『後ろから来た矢は当たらない説』
走っている人を矢で打つと、放たれた矢がその人のところに届く時間に、その人は少し移動する。人が移動した距離を矢が進む間、人はわずかに移動してる。これを永遠に繰り返しても、人と矢の距離は縮むだけで矢は人の体を貫くことはない・・・・。って、実際は当たりまくりだ。
概念そのものが違うから、この理論上で説明するのは難しい。
追いかけると先行した者がちょっと動くという条件自体が特殊だし、先行した者の背中という特異点が起点だから、その”ゼロ”点を超えられない。
ちなみに社内でこの問題を出した。
答えは、
「どうせ戻ってくるなら、A地点で月見バーガー食べて待ってます。」
と、途中で寝るウサギの話を超越して、『全工程、寝て過ごす』強者や、
「A点-B点って話を聞くと、昔のP点の事を思い出す。」
って、元彼の思い出のように語り話が出たり。
確かに、関数や図形では、Q点、P点が良く出てきた。
なぜQ点、P点??
P点って、建築施行会社の総合評定値(P点)と言うのもあるらしい。
日本では、いろんな”点”が使われているようだ。
で、話を元に戻して、時速5kmで走るウサギさんがいます。
彼は、どこまでも時速5Kmで走り続けます。
彼のライバル、カメさんは足が遅く、はじめは時速4Kmで、下りの復路は時速6Kmでペースアップが可能です。
箱根駅伝のごとく、初日は往路でウサギ時速5Km、カメ時速4Kmで走り、
翌日復路は、ウサギ時速5Km、カメ時速6Kmで走ります。
カメは、ウサギを追い抜くことが出来るでしょうか。
A地点を出発して、良く判らない距離のB地点まで走り、同じ距離をもとってくる。
時速は、1時間あたり何キロ進むかって事なので、時間で距離を割る。
距離を何時間で走ることが出来るかは、距離を時速で割ると、時間が出てくる。
5Kmの距離を時速5Kmで走ると、1時間だろうなぁ、10Kmなら2時間かかるなぁって、なんとなくみんな計算してる。
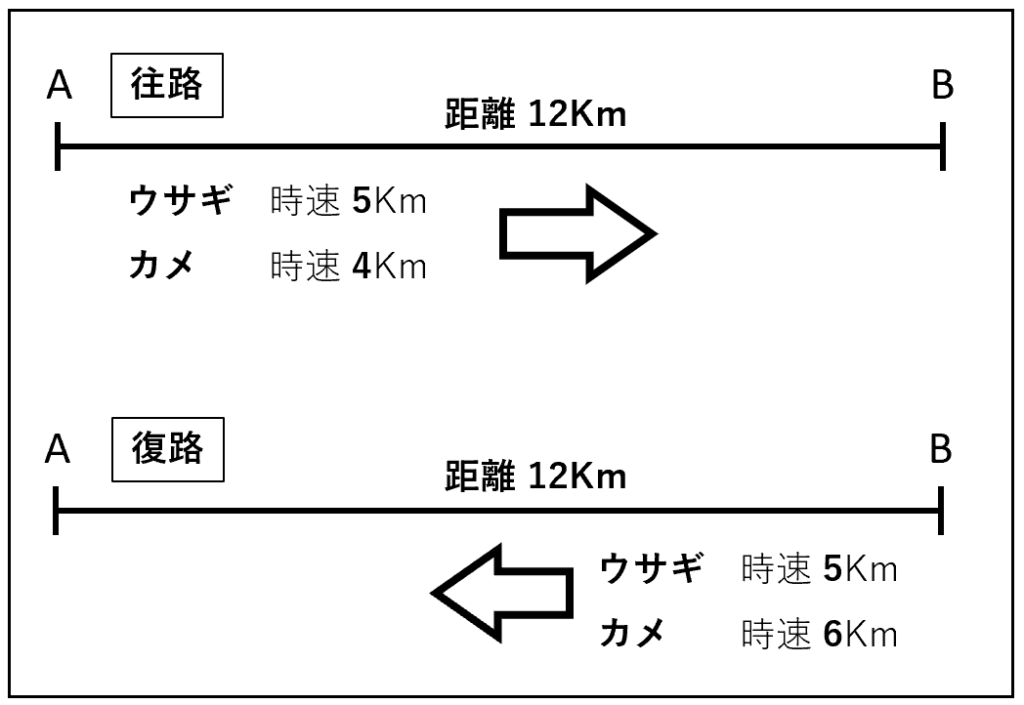
仮にA-B間の距離を12Kmとすると、移動にかかる時間は、
[往路]
ウサギ : 12Km ÷ 時速 5Km = 2.4時間
カメ : 12Km ÷ 時速 4Km = 3時間
ウサギは30分以上早く到着して、箱根の温泉を堪能している計算だ。
敗北感を知ったカメは翌日リベンジを誓う。
[復路]
ウサギ : 12Km ÷ 時速 5Km = 2.4時間
カメ : 12Km ÷ 時速 6Km = 2時間
見事リベンジを果たしたカメは、ご満悦だ。
結果、何分かかったかというと、
ウサギ : 4.8時間
カメ : 5時間
12分、ウサギが早い。往復の距離は24Km。
それぞれの平均時速は、・・・ウサギはずっと時速5Kmだから、計算の必要は無いけれど、
[平均時速]
ウサギ : 24Km ÷ 4.8時間 = 時速 5Km
カメ : 24Km ÷ 5時間 = 時速 4.8Km
で、カメが遅いことがわかる。
じゃぁ、完全リベンジするには、カメは復路で時速何Km以上出せば良いかというと、
ウサギの全体の時間から、カメが往路で使った時間の残りの時間で、復路を走りきれば、ウサギと同着で到着できる。
つまり、
ウサギの全時間 4.8時間 – 往路のカメの時間 3時間 = 1.8時間
この1.8時間で12Kmを走りきれば、カメは勝てる。
12Km ÷ 1.8時間 = 時速6.67Km
結構頑張らないと、カメはウサギに勝てない。
リベンジには、努力が必要だ。
考え方や計算は小学生レベルで簡単なんたけど、先行したウサギを追いかけるのに
「時速6Kmで走れば、追いつくんじゃねぇ??」
と言うわけにはいかないところが、ミソだ。
「あっ、ちょっと用があるから先に行っていて。後から追いかけるから。」
と言う人が、いっこうに現れる気配が無いことが良くあるけれど、似たような現象かもしれない。
しかも、車で遠出するときは、早朝よりも昼間の方が道が混んでいて、全く追いつく事は出来ない。
「いやぁ、道が混んでいて。」
「すぐ終わる用事か、なんかトラブって。」
「追いつこうとしたんだけど、眠くて途中のサービスエリアで寝てた。」
大人は、たくさんのファクターという特異点を乱立させて、概念そのものを換えてしまうテクニックで時間を稼ぐ。